Виды многогранников
- Многогранников разновидностьВыпуклый многогранник

В выпуклом многограннике прямая линия может только разрезать поверхность в двух точках. Вогнутый
В вогнутом многограннике прямая линия может срезать поверхность более чем в двух точках.
Регулярные
Правильный многогранник состоит из углов и граней (правильных многоугольников), которые равны.
Платонные твердые тела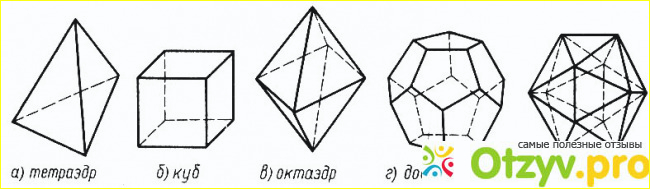
Платонные твердые тела являются выпуклыми правильными многогранниками.
Существует ровно пять типов платоновых тел: Тетраэдр. Гексаэдр или куб. Октаэдр. Додекаэдр. Икосаэдр. Нерегулярные Неправильный многогранник определяется многоугольниками, которые состоят из элементов, которые не все равны.
Типы многогранников по количеству лиц Вы когда-нибудь играли в игру с чем-то вроде полиэдры? Скорее всего, у вас есть, даже если вы никогда не слышали этого термина.
Если вы когда-либо играли в Yahtzee, Boggle или любую другую игру с участием пары шестигранных кубиков, вы играли с полиэдрами. Это потому, что шестигранный кубик на самом деле является типом многогранников, называемых кубом . Когда вы посмотрите вокруг, вы заметите, что в вашей повседневной жизни много многогранников, многие из них односторонние, как приборы и коробки. Что такое многогранники? Многогранники - очень общие формы. Даже фигуры, которые не являются многогранниками, могут быть смоделированы полиэдрами; на самом деле, это то, что происходит во многих компьютерных графиках. Так что это? Многогранникипредставляют собой трехмерные объекты из полигонов. Многоугольники представляют собой двумерные объекты, выполненные из прямых линий; они могут быть квадратами, прямоугольниками, треугольниками, неуголами и т. д. Есть три словаря слова, которые важны для запоминания, чтобы понять, какие многогранники: грани , ребра и вершины.
Лица - это плоские части многогранников - это многоугольники. Края - это линия, где встречаются две грани. Вершины - это точки, где встречаются три или более лица. На самом деле существует математическая связь между этими тремя терминами, известными как формула многогранника Эйлера .
1. Он утверждает, что вершины, ребра и грани удовлетворяют уравнению: Вершины - Края + Лица = 2. Типы многогранников Таким образом, единственными требованиями для полиэдра являются то, что все грани многогранника являются многоугольниками и что все грани всех граней совпадают, поэтому нет пробелов.
2. Ниже приведен пример регулярного многогранника этот называется додекаэдром . Додекаэдр является регулярным многогранником, где все грани являются регулярными пятиугольниками. Многогранники не обязательно должны быть регулярными, что означает, что все грани одинаковы, и все полигоны являются регулярными. Многогранник представляет собой трехмерную замкнутую поверхность или твердое тело, ограниченную плоскими фигурами, называемыми полигонами .
3. Слово многогранник происходит от греческого префикса poly- , что означает «много», а слово hedron - «поверхность». Многогранник - это твердое тело, границы которого состоят из плоскостей. Многие общие объекты в окружающем нас мире находятся в форме многогранников. Куб виден во всем: от кубиков до часовых радиостанций; CD-чехлы и палочки с маслом находятся в форме многогранников, называемых параллельными пипедами. Пирамиды - это тип многогранника, как и геодезические купола.
4. Большинство образованных в природе форм нерегулярны. Однако в интересном исключении кристаллы растут в математически совершенных и часто сложных многогранниках. Ограничивающие многоугольники многогранника называются гранями. Отрезки линий, вдоль которых встречаются грани, называются ребрами. Точки, в которых концы краев пересекаются (думают о углу коробки с зерном), являются вершинами. Вершины связаны через тело многогранника воображаемой линией, называемой диагональю. Многогранник классифицируется как выпуклый, если диагональ содержит только точки внутри многогранника. Выпуклые многогранники также известны как многогранники Эйлера и могут быть определены уравнением E = v + f - e = 2, где v - число вершин, f - число граней, e - число ребер. Пересечение плоскости и многогранника называется сечением многогранника. Сечения выпуклого многогранника - все выпуклые многоугольники. Многогранники классифицируются и обозначаются в соответствии с количеством и типом граней. Многогранник с четырьмя сторонами является тетраэдром , но также называется пирамидой .
5. Шестигранный куб также называетс я гексаэдром. Многогранник с шестью прямоугольниками как стороны также имеет много имен - прямоугольную параллелепипедную прямоугольную призму или коробку. Другие общие многогранники лучше всего описываются так же, как и ранее названные, которые частично отключаются или усекаются плоскостью. Представьте себе, что вырезать углы куба, чтобы получить, например, многогранник, образованный из треугольников и квадратов. Многогранник - это твердое тело, которое построено многоугольниками. Существует много разных типов многогранников. Двумя наиболее известными группами являются платонические твердые тела и архимедовы тела. Пять платоновых твердых тел. Архимедовы твердые тела Существует группа полиэдров. ( кубокатерон, большой ромбико, меньший ромбико) ( икосидодекаэдр, большой ромбикозидодекаэдр, меньший ромбикозидодекаэдр) (кубик, окунь,) Как только полиэдр будет построен, вы можете растянуть края каждой поверхности многоугольника до тех пор, пока они не соберутся. Этот процесс называется стеллацией. Однако одна звезда (стелла-октангула), три додекаэдровых стеллажа (мелкие сериализованные, великие звездчатые и великие додекаэдры) и 58 звездный икосаэдр. Эти звездчатые многогранники уступают место твердым течениям Кеплера-Поинсо .
я гексаэдром. Многогранник с шестью прямоугольниками как стороны также имеет много имен - прямоугольную параллелепипедную прямоугольную призму или коробку. Другие общие многогранники лучше всего описываются так же, как и ранее названные, которые частично отключаются или усекаются плоскостью. Представьте себе, что вырезать углы куба, чтобы получить, например, многогранник, образованный из треугольников и квадратов. Многогранник - это твердое тело, которое построено многоугольниками. Существует много разных типов многогранников. Двумя наиболее известными группами являются платонические твердые тела и архимедовы тела. Пять платоновых твердых тел. Архимедовы твердые тела Существует группа полиэдров. ( кубокатерон, большой ромбико, меньший ромбико) ( икосидодекаэдр, большой ромбикозидодекаэдр, меньший ромбикозидодекаэдр) (кубик, окунь,) Как только полиэдр будет построен, вы можете растянуть края каждой поверхности многоугольника до тех пор, пока они не соберутся. Этот процесс называется стеллацией. Однако одна звезда (стелла-октангула), три додекаэдровых стеллажа (мелкие сериализованные, великие звездчатые и великие додекаэдры) и 58 звездный икосаэдр. Эти звездчатые многогранники уступают место твердым течениям Кеплера-Поинсо .
Твердые тела Кеплера-Поинсо состоят из четырех вогнутых многогранников с пересекающимися лицевыми плоскостями. Кеплер обнаружил два из четырех (маленький звездчатый додекаэдр и великий звездчатый додекаэдр) около 1619 года, в то время как Пуансо вновь открыл эти два и обнаружил еще два (великий додекаэдр и великий икосаэдр) в 1809 году. Выпуклые многогранники хорошо определены, с несколькими эквивалентными стандартными определениями. Однако формальное математическое определение многогранников, которые не должны быть выпуклыми, было проблематичным. Многие определения «полиэдра» были даны в определенных контекстах, [1] более строгие, чем другие, и не существует универсального соглашения о том, какие из них выбрать. Некоторые из этих определений исключают формы, которые часто считаются полиэдрами (такими как самопересекающиеся многогранники ) или включают формы, которые часто не считаются допустимыми многогранниками (такими как твердые тела, границы которых не являются многообразиями ).
Как заметил Бранко Грюнбаум , «Оригинальный грех в теории многогранников восходит к Евклиду, а через Кеплера, Пуансота, Коши и многих других ... на каждом этапе ... писатели не смогли определить, что такое многогранники». [2] Тем не менее, существует общее согласие в том, что многогранник представляет собой твердое тело или поверхность, которые могут быть описаны его вершинами (угловыми точками), ребрами (отрезки, соединяющие определенные пары вершин), гранями(двумерные многоугольники ), а иногда и тремя -мерный внутренний объем . Можно различать эти различные определения в зависимости от того, описывают ли они полиэдр как твердое тело, независимо от того, описывают ли они его как поверхность, или описывают ли они его более абстрактно на основе его геометрии падения . Общим и несколько наивным определением многогранника является то, что он является телом, граница которого может быть покрыта конечным числом плоскостей [3] [4], или что это твердое тело, образованное как объединение конечного числа выпуклых многогранников. [5]
Естественные уточнения этого определения требуют, чтобы твердое тело было ограничено, имело связную внутренность и, возможно, также имело связную границу. Границы такого многогранника могут быть определены как связанные компоненты частей границы внутри каждой из покрывающих его плоскостей, а ребра и вершины - как отрезки и точки, где встречаются грани. Однако многогранники, определенные таким образом, не включают самопересекающиеся звездчатые многогранники, их лица могут не образовывать простые многоугольники, а некоторые ребра могут принадлежать более чем двум граням. [6]
Определения, основанные на идее ограничивающей поверхности, а не твердого тела, также являются общими. [7] 
Например, О'Рурк (О'Рурк, 1993) определяет многогранник как объединение выпуклых многоугольников (его граней), расположенных в пространстве, так что пересечение любых двух многоугольников является общей вершиной или ребром или пустым множеством, и поэтому их объединение является многообразием . [8]
Если плоская часть такой поверхности сама по себе не является выпуклым многоугольником, О'Рурк требует ее подразделить на более мелкие выпуклые многоугольники с плоскими двугранными углами между ними. В более общем плане Грюнбаум определяет акоптический многогранникбыть набором простых многоугольников, которые образуют вложенное многообразие, причем каждая вершина инцидентна, по крайней мере, трем ребрам и каждой из двух граней, пересекающихся только в общих вершинах и ребрах каждого из них. [9]Кромвель дает аналогичное определение, но без ограничения трех ребер на вершину. Опять же, этот тип определения не охватывает самопересекающиеся многогранники. [10]
Подобные понятия составляют основу топологических определений многогранников как разбиений топологического многообразия на топологические диски (грани), попарные пересечения которых должны быть точками (вершинами), топологическими дугами (ребрами) или пустым множеством. Однако существуют топологические многогранники (даже со всеми гранями граней), которые не могут быть реализованы в виде акоптических многогранников.[11]
Один современный подход основан на теории абстрактных многогранников . Их можно определить как частично упорядоченные множестваэлементами которого являются вершины, ребра и грани многогранника. 
Элемент вершины или края меньше элемента edge или face (в этом частичном порядке), когда вершина или ребро являются частью ребра или грани. Кроме того, можно включить специальный нижний элемент этого частичного порядка (представляющий пустой набор) и верхний элемент, представляющий весь многогранник. Если части частичного порядка между элементами на трех уровнях друг от друга (то есть между каждой гранью и нижним элементом и между верхним элементом и каждой вершиной) имеют ту же структуру, что и абстрактное представление многоугольника, то эти частично упорядоченные множества несут точно такую же информацию, как топологический многогранник. Однако эти требования часто расслабляются,[12]
(Это означает, что каждое ребро содержит две вершины и принадлежит двум граням и каждая вершина на грани принадлежит двум ребрам этой грани.)
Геометрические многогранники, определенные другими способами, могут быть описаны абстрактно таким образом, но также можно использовать абстрактные полиэдры в качестве основы определения геометрических многогранников. Реализация абстрактного многогранника обычно берутся отображение из вершин абстрактного многогранника до геометрических точек, такимчто точки каждой грани лежатодной плоскости. Тогда геометрический многогранник можно определить как реализацию абстрактного многогранника. [13]
Также были рассмотрены реализации, которые отказываются от требования планарности, которые налагают дополнительные требования симметрии, или которые отображают вершины в пространства с большими размерами. [12]
В отличие от твердотельных и поверхностных определений, это отлично работает для звездных полиэдров.
Однако без дополнительных ограничений это определение допускает вырожденные или неверные многогранники (например, путем отображения всех вершин в одну точку), и вопрос о том, как сдерживать реализации, чтобы избежать этих вырождений, не был решен.
Во всех этих определениях полиэдр обычно понимается как трехмерный пример более общего многогранника в любом числе измерений. Например, многоугольник имеет двумерное тело и никакие грани, а 4-многогранник имеет четырехмерное тело и дополнительный набор трехмерных «ячеек».
Однако в некоторых литературе по многомерной геометрии термин «многогранник» означает нечто иное: не трехмерный многогранник, а форма, которая в некотором роде отличается от многогранника.
Например, некоторые источники определяют выпуклый многогранник как пересечение конечного числа полупространств , а многогранник - ограниченный многогранник. [14] [15] Остальная часть этой статьи рассматривает только трехмерные многогранники.
Видео обзор
| Все(5) |
|---|
 геометрия МНОГОГРАННИКИ 9 и 10 класс геометрия МНОГОГРАННИКИ 9 и 10 класс |  Геометрия 10 кл Элементы симметрии правильных многогранников Геометрия 10 кл Элементы симметрии правильных многогранников |  ЕГЭ математика. Объем и площадь поверхности многогранников ЕГЭ математика. Объем и площадь поверхности многогранников |  Геометрия 10 кл Понятие многогранника Геометрия 10 кл Понятие многогранника |  Геометрия 10 кл Призма Геометрия 10 кл Призма |




Комментарии на отзыв: