Примеры алгоритмов
- АлгоритмыПримеры алгоритмов
Алгоритм определяет ряд шагов, которые выполняют определенную задачу вычисления или. Алгоритмы были первоначально рождены как часть математики - слово «алгоритм» происходит от арабского писателя Мухаммада ибн Муса, но в настоящее время это слово тесно связано с информатикой. В этой книге мы рассмотрим несколько различных алгоритмов для выполнения множества задач.
Алгоритмы напоминают рецепты.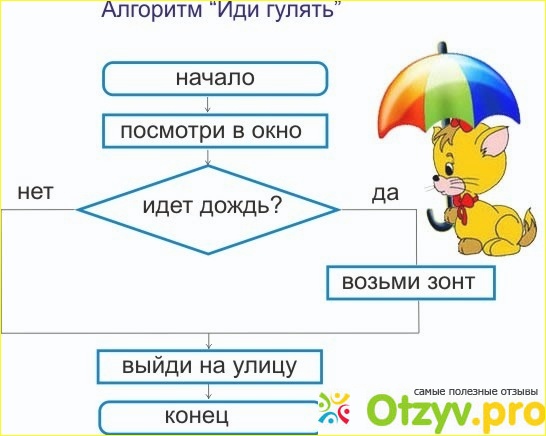
1.
Рецепты рассказывают вам, как выполнить задачу, выполнив ряд шагов. Например, чтобы испечь торт, выполните следующие шаги: предварительно разогрейте духовку; смешайте муку, сахар и яйца; влить в форму для выпечки; и так далее.
2. В рецепте такой шаг, как «Выпекать до завершения», является неоднозначным, потому что он не объясняет, что означает «сделано». Более ясное описание, такое как «Испечь, пока сыр начинает пузыриться», лучше. В вычислительном алгоритме такой шаг, как «Выбрать большое число», является неопределенным: что такое большой? 1 миллион, 1 миллиард, или 100? Должен ли быть каждый раз каждый раз, или один и тот же номер может использоваться при каждом запуске?
· Алгоритм ожидает определенный набор входов. Например, это может потребовать двух чисел, где оба числа больше нуля. Или может потребоваться слово или список из нуля или более чисел.
· Алгоритм создает определенный набор выходов. Он мог бы выводить большее из двух чисел, версию в верхнем регистре слова или отсортированную версию списка чисел.
· Гарантируется, что алгоритм завершит и произведет результат, всегда останавливаясь после конечного времени. Если бы алгоритм мог запускаться вечно, это было бы не очень полезно, потому что вы никогда не сможете получить ответ.
· Большинство алгоритмов гарантируют получение правильного результата. Это редко бывает полезно, если алгоритм возвращает наибольшее число 99% времени, но 1% времени, когда алгоритм терпит неудачу и вместо этого возвращает наименьшее число.
· Если алгоритм накладывает требование на его входы (называемое предварительным условием), это требование должно быть выполнено. Например, предварительным условием может быть то, что алгоритм принимает только положительные числа в качестве входных данных. Если предварительные условия не выполняются, тогда алгоритм может выйти из строя, производя неправильный ответ или никогда не заканчивая.
Изучение алгоритмов является фундаментальной частью информатики. Существует несколько различных характеристик алгоритма, которые полезно знать:
1. Существует ли алгоритм для выполнения данной задачи?
2. Если кто-то предлагает алгоритм для решения задачи, уверены ли мы, что алгоритм работает для всех возможных входов?
3. Как долго выполняется алгоритм? Сколько пространства памяти требуется?
4. Как только мы узнаем, что можно решить проблему с помощью алгоритма, естественный вопрос заключается в том, является ли алгоритм наилучшим. Можно ли решить проблему быстрее?
Большинство из этих вопросов будут обсуждаться для алгоритмов, рассмотренных в этой книге.
Примерный алгоритм
Давайте рассмотрим очень простой алгоритм
Проблема: если список положительных чисел, верните наибольшее число в списке.
Входы: список положительных чисел. Этот список должен содержать хотя бы одно число. (Просить наибольшее число в списке номеров не является значимым вопросом.)
Выходы: число, которое будет наибольшим числом списка.
Алгоритм:
1. Установите значение 0.
2. Для каждого номера в списке сравните его. Если размер больше, установите значение.
3. Теперь установлено на наибольшее число в списке.
Соответствует ли это критериям для алгоритма?
· Это однозначно? Да. Каждый шаг алгоритма состоит из примитивных операций, и перевод каждого шага в код Python очень прост.
· Определяет ли он входы и выходы? Да.
· Гарантировано ли это прекращение? Да. Список имеет конечную длину, поэтому после просмотра каждого элемента списка алгоритм остановится.
· Получает ли он правильный результат? Да. В формальной обстановке вы должны обеспечить тщательное доказательство правильности. В следующем разделе я опишу доказательство альтернативного решения этой проблемы.
Рекурсивная версия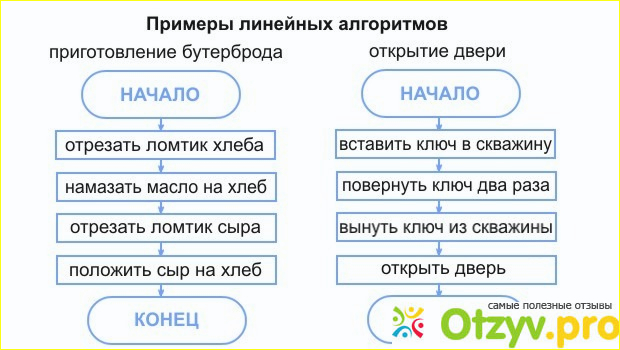
Для решения одной и той же задачи может быть много разных алгоритмов. Вот альтернативный алгоритм
Наконец, дает ли он правильный результат? Да.
Рассмотрим список длины 1. В этом случае наибольшее число также является единственным числом в списке возвращает это число, поэтому оно корректно для списков длины 1.
Теперь рассмотрим более длинный список длины, где произвольная длина. Предположим, что мы доказали, что это правильно для всех списков длины. Следовательно, значение будет самым большим значением в остальной части списка. Есть два случая, о которых нужно беспокоиться.
· Случай 1: первый элемент списка - самый большой элемент. В этом случае в списке больше нет других значений Мы предполагаем, что это правильно, когда выполняется в остальной части списка, поэтому возвращаемое значение будет меньше Поэтому сравнение будет истинным, поэтому первая ветка будет взята, возвращаясь. Это самый большой элемент в списке, поэтому в этом случае алгоритм правильный.
· Случай 2: первый элемент списка не самый большой элемент. В этом случае в списке есть хотя бы одно значение, которое больше верна для сокращенной версии остальной части списка, возвращая максимальное значение и она содержит, поэтому это значение должно быть больше Поэтому сравнение будет ложным, поэтому ветвь будет взята, возвращаясь, самое большое значение в остальной части списка. В этом случае предполагается, что это не самое большое значение, поэтому это самое большое значение, и алгоритм также является правильным в этом случае.
В этих двух случаях мы теперь показали, что если верно для списков длины, это также верно для списков длины В первой части нашего аргумента мы показали, это правильно для списков длины 1. Поэтому это также верно для списков, которые содержат 2 элемента, и 3 элемента и 4, 5, 6, ... до любой номер.
Это может показаться трюком; мы показали, что это правильно для тривиального случая одно элементного списка, а затем показали, что он корректен в задаче определенного размера. Такие доказательства называются индуктивными доказательствами, и они являются общеизвестным математическим методом доказательства теоремы.
Проведение индуктивного доказательства некоторого свойства требует двух шагов.
1. Во-первых, вы показываете, что свойство истинно для некоторого простого случая: пустой список или список длины 1, пустой набор, одна точка. Обычно эта демонстрация очень проста; часто очевидно, что свойство истинно. Это называется базисным случаем.
2. Затем вы предполагаете, что свойство истинно для размера N и показывает, что оно верно для некоторых больших размеров, таких как N + 1. Это называется индуктивным шагом и, как правило, более сложным.
Как только у вас есть обе демонстрации, вы доказали, что свойство верно для бесконечного числа значений N; правильность для N = 1 означает, что случай N = 2 также верен, что, в свою очередь, подразумевает правильность для N = 3, 4, 5 и любого другого положительного целого. Не всякая теорема может быть введена в форму, где можно использовать индуктивное доказательство.
Видео обзор
| Все(5) |
|---|
 Примеры алгоритмов Примеры алгоритмов |  Примеры рекурсивных алгоритмов Примеры рекурсивных алгоритмов |  Урок: Исполнитель Чертежник. Пример алгоритма Урок: Исполнитель Чертежник. Пример алгоритма |  Примеры реализации алгоритмов размещения Примеры реализации алгоритмов размещения |  4. Алгоритмы в Подвесном. Мастер-метод, примеры, подсчет количества инверсий. 4. Алгоритмы в Подвесном. Мастер-метод, примеры, подсчет количества инверсий. |





Комментарии на отзыв: